综合排名问题是一个多变量分析技术!
近一时期排名非常时髦,形成了排名经济,比如:胡润富人排行榜,财富500强,慈善排名,城市竞争力排行,MBA商学院排名,大学排行榜等等!最近刚刚完成广播电视节目综合评估体系客体评估项目,其中也涉及到电视节目的综合评估问题,特别是综合排名问题。大部分情况下综合评价问题都会涉及到排名,多指标排名问题。
记住:市场研究或作研究的人从来不排名,只是做研究往往需要排名!
综合排名是一项系统综合评估研究方法,焦点是如何科学、客观地将一个多维度、多评价指标问题综合成为一个单指标形式,利用产生的综合评价指数进行排名和评价。
综合排名的的形成需要研究人员对评价对象进行大量基础性数据分析基础上,并依据专业知识和评价方法的认识,确定评估指标体系,对每个评价指标在综合评价体系中的重要程度进行测算。研究人员需根据各指标的重要性确定了权重,据此对每项不同测量尺度指标进行修正后加权并标准化无量纲,最终采用多元统计分析方法对评价指标进行了系统最佳综合,形成最终综合评价。
主要包括以下几个方面:
-
评估对象确定
-
评估范围
-
评估分类
-
评估指标体系
-
评估权重
-
评估指标标准化
-
综合方法
-
评估周期
-
评估发布
综合评估问题涉及面比较广,下面我们仅仅就综合排名问题讲讲,我们采用大学研究生排行榜的数据进行综合排名!我收集了某年的大学研究生排行榜,因为显示的问题我仅仅截取了前20名,人民大学提到了前面进入第20名!(数据源已经记不清楚出处了)
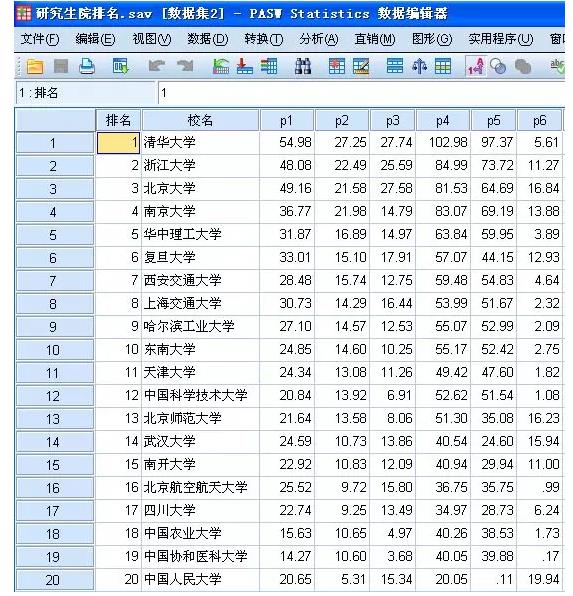 从上面我们可以看到:20家大学研究生院的综合排名情况,最左边一列是最初的排名,这个排名名次是按照六个指标得到了,六个指标分别是:
从上面我们可以看到:20家大学研究生院的综合排名情况,最左边一列是最初的排名,这个排名名次是按照六个指标得到了,六个指标分别是:
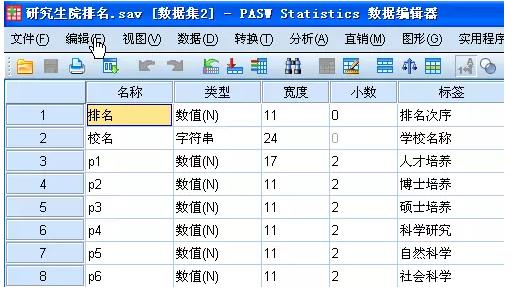 我这里并不关心这六个指标如何获得,和数据准确性问题,我们只关心应该如何在现有指标下进行综合排名问题!
我这里并不关心这六个指标如何获得,和数据准确性问题,我们只关心应该如何在现有指标下进行综合排名问题!
当然,大家要关注这六个指标的测量尺度,取值范围,量纲的大小等,你将来总不希望把吨和克进行相加吧!
方法一:等权重求和法 T1
我们先来看看,把现在六个指标求和,得到T1=P1+P2+P3+P4+P5+P6,然后按T1降序排名;
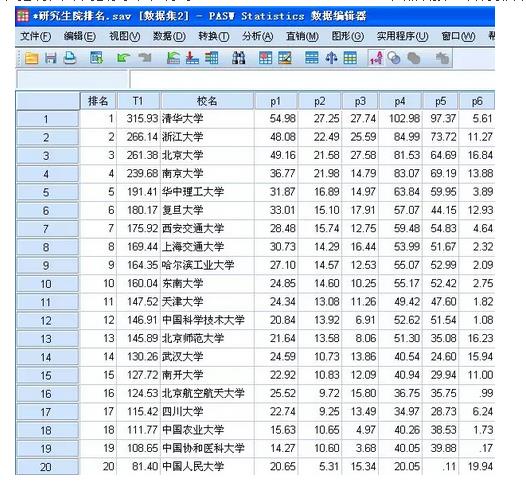
看到了吗?该排行榜的发布就是用的加法,最简单的方法!
从数据看以看出,指标P6与其它指标单位差异较大,简单相加有缺陷,但是这种方法是大家最常用的,比如:高考录取分数就是各门考试成绩加总,得到总成绩(高考成绩),根据录取人数取得分位点,然后确定录取分数线,并排名从高到底录取;当然硕士研究生录取也是这种方法!
为什么要用这种方法呢?如果用复杂多变量方法,得到总指标排名,估计家长们或学生都要疯了,都不知道自己如何能够被录取,算法不懂,怎么被录取!显然,其它方法是不能采用的,这是最好的可执行方案!
方法二:主观加权求和法 T2
但是,录取单位总是想能不能把偏科的人录取,比如我看重数学、物理,这两个指标应该权重更大些,比如我们假设考了6门课,我们根据经验、主观判断、领导指示或专家评估最终确定:30:25:20:15:10:5的权重!
再次计算;T2=p1 * 0.30 + p2 * 0.25 + p3 * 0.20 + p4 * 0.15 + p5 * 0.10 + p6 * 0.05
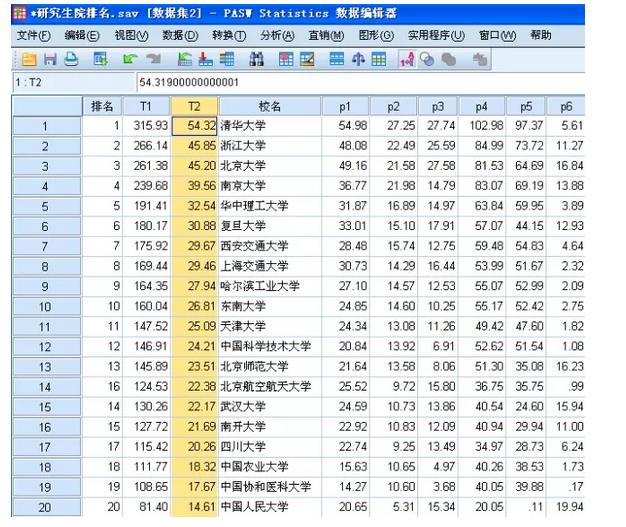 我们按照T2降序排列,看一下排名,基本次序是一致的,只是在15名附近发生一点改变!
我们按照T2降序排列,看一下排名,基本次序是一致的,只是在15名附近发生一点改变!
如果按照这种方式排名,首先所有指标应该在同一个量纲上,经常是在指标都是在100分制下,并且权重最好合计为1,最终得到的排名总分也是同样量纲和尺度!
这种情况最适合综合评价方式,加权平均啦!当然如何确定权重就成为关注的要点,科学性、合理性都需要明确!大部分综合评估方法在最后都是采用这种排名方法!
方法三:秩综合排名法 T3
什么是秩,秩序就是求次序!所有我们可以计算每个指标的秩,然后根据秩的大小进行求和!
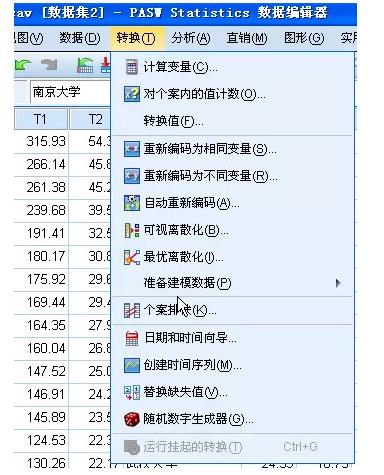 从SPSS软件可以选择个案排秩,指定最大值=1,我们可以得到六个指标的秩指标次序!我们采用简单加法求和和排名,看看结果如何?
从SPSS软件可以选择个案排秩,指定最大值=1,我们可以得到六个指标的秩指标次序!我们采用简单加法求和和排名,看看结果如何?
计算 T3=Rp1 + Rp2 + Rp3 + Rp4 + Rp5 + Rp6,按照T3升序排列!
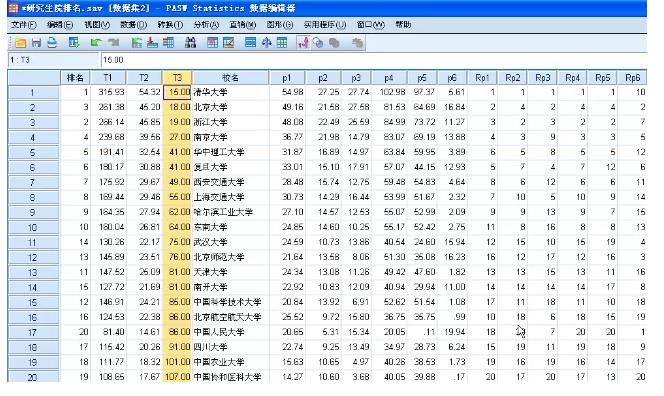 从T3升序排列看,这时候大致排名与原始没有发生颠覆性变化,只是在前后名次上有了一定改变!
从T3升序排列看,这时候大致排名与原始没有发生颠覆性变化,只是在前后名次上有了一定改变!
这种方法也是一种排名方法,经常用在比如世界杯最佳阵容或最佳球队评选上,假如有六个记者或专家给所有球队或球员选出最佳阵容或球队时,往往比较可操作的方法是让所有评价者给评价对象打分或者排名,排名更好操作,然后求和!
注意:往往评价者只会评出他最熟悉的,可能会产生缺省值问题,所以要根据每个评价者的情况和缺失情况进行缺省值处理!然后进行求和!
方法四:主成分排名法 T4
这种方法就是多变量分析技术了,主成分分析方法经常用来进行综合评估和排名!有关主成分分析技术的相关内容我将在主成分分析专题讲,这里还是关注如何进行排名!
主成分分析是根据指标和数据得到第一主成分,并根据第一主成分得分进行排名的方法!因为,第一主成分往往是凝聚了所有变量的最大变差,也就是解释了6个指标的最大差异(解释度),或者说最大综合成分,排名就是找差异吗?据此排名!
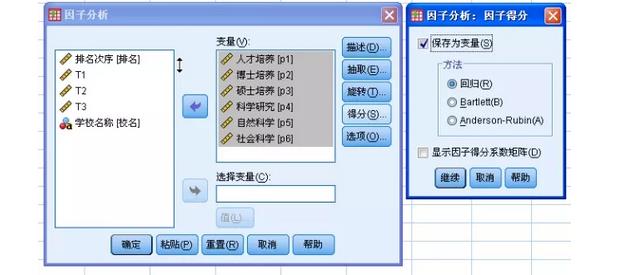 SPSS软件没有专门命名主成分分析,是与因子分析整合的,在选择因子分析后,只要不进行旋转,就可以得到主成分分析结果,记住把得分保存下来,我们可以要求保存所有主成分,六个指标得到六个主成分,但我们只要保存前两个就可以了!
SPSS软件没有专门命名主成分分析,是与因子分析整合的,在选择因子分析后,只要不进行旋转,就可以得到主成分分析结果,记住把得分保存下来,我们可以要求保存所有主成分,六个指标得到六个主成分,但我们只要保存前两个就可以了!
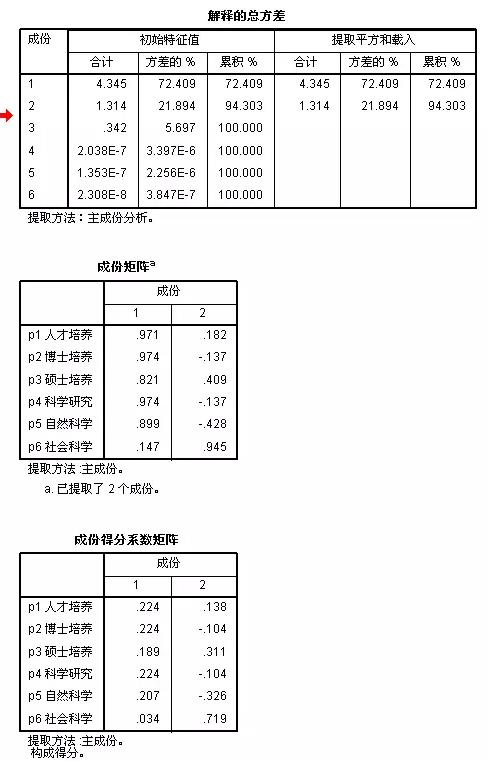 从主成分可以看出:第一主成分解释了6个指标变差的72.409%,把保存的第一主成分按降序排列,我们看一下排名情况;
从主成分可以看出:第一主成分解释了6个指标变差的72.409%,把保存的第一主成分按降序排列,我们看一下排名情况;
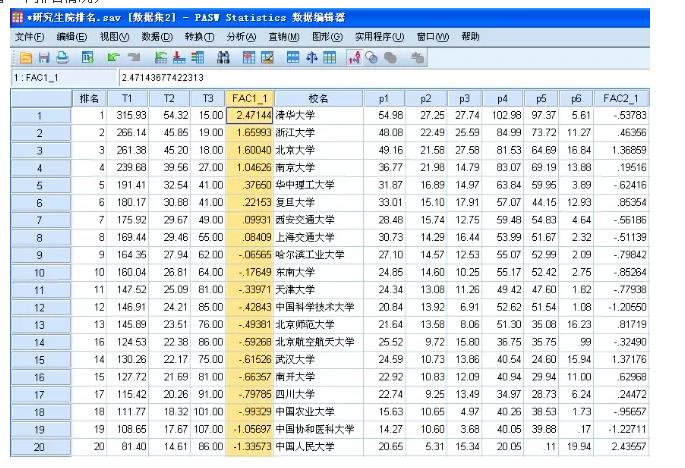 从排名顺序我们看到,这种方法与方法二加权排名几乎一样,当然与简单求和也基本一致!这说明,这种方法是能够得到理想的综合排名的!(理论上说,如果排名对象差异很大,不同方法得当的结果基本一致!)
从排名顺序我们看到,这种方法与方法二加权排名几乎一样,当然与简单求和也基本一致!这说明,这种方法是能够得到理想的综合排名的!(理论上说,如果排名对象差异很大,不同方法得当的结果基本一致!)
同时,你可以看到,成分得分系数矩阵的第一主成分列,实际上就是基于数据驱动的权重啦,所以这种方法不需要事先得到主观权重,完全数据驱动!但是,得到的只是排名,具体的排名得分没有实际意义了,如果你希望得到排名的得分具有实际意义,显然该方法会把人搞糊涂!但是我们也可以把主成分得分进行数值变化或映射,得到指数或什么规范得分!
说明:你也可以按照第二主成分进行排名,但这个时候完全不同了!
这里我们可以得到另外一种收获,就是可以按照第一主成分和第二主成分进行散点图分析,得到直观分析!
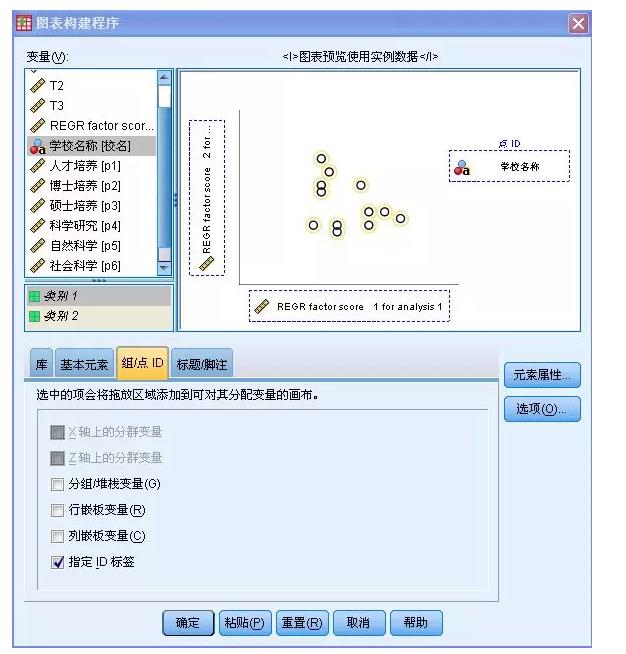
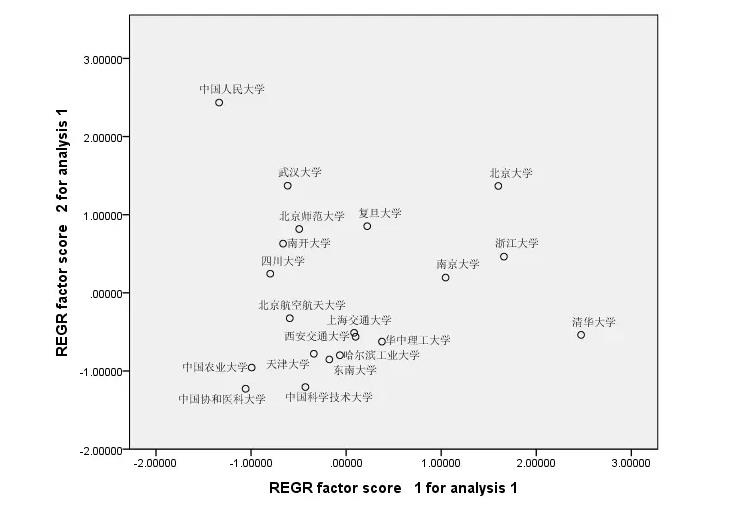 你会看这种图吗?
你会看这种图吗?
方法五:主成分综合加权法 T5
我们从上面一种排名方法看到,虽然按照第一主成分进行了排名,但第二主成分也解释了21.894%,如果综合将可以解释数据的94.303%;(学术研究有时候更追求高解释度),好了,现在我们可以按照主成分的解释度作为权重,把两个主成分进行加权求和!
计算:T5=FAC1_1 * 72.409 + FAC2_1 * 21.894
我们看看排名情况:
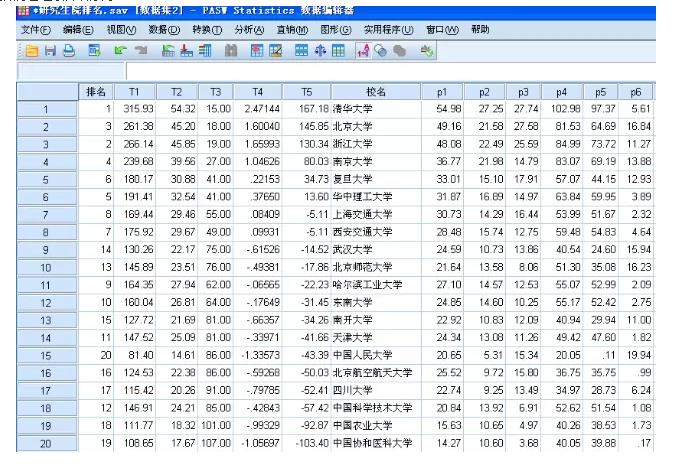 对照着第一列的原始排名,这时候排名结果发生了改变,特别是人民大学前进了几名!
对照着第一列的原始排名,这时候排名结果发生了改变,特别是人民大学前进了几名!
这时候,我们要看看排名的指标对排名的意义和影响了,我们可以分析看出,6个评价排名指标实际上主要是两个维度,简单说就是自然科学和社会科学维度,前面四种排名方法基本上权重都在自然科学维度上,第五种方法考虑了社会科学维度!
我们看一下因子分析结果,采用最大方差旋转!
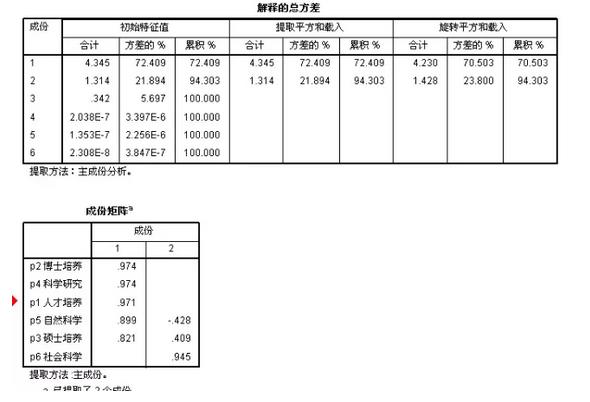
显然,第一因子我们命名为:自然科学,第二因子命名:社会科学
所以,我说我们学校总是不能进入排行榜呢?原来所谓的排行榜就是看自然科学(工科类)的排名啊!哈哈!
针对我们文科和艺术类学校,只能垫底啦!下次我要是排名,一定想法用复杂的排名技术,把我们学校排进去,相信我能做到这一点!或者咱们来个分类排名,反正咱有技术!开玩笑啦!
记住一点:方法五在采用的时候一定格外小心,因为主成分是正交的,不同方向能否综合要记住,也就是数值越大越表示好,也就是两个指标具有数值同向,才有可能满足线性可加性!不行还是方法四比较妥当!
方法六:乘法原则
在指标同是正向,我们也可以将各个指标相乘,值越大排名考前!乘法原则主要用在:一票否决,或某些指标是另一个指标的修正因子!
方法七:其它方法
你还可以采用部分乘法原则与加法原则综合法,也可以因子得分进行排名,因子得分加权排名,所有主成分或因子加权排名等等!
排名方法大致就介绍到这里了,我的工作也就完成了!
至于排行榜的发布,商业的、行政的、领导的、媒体的、企业的各种因素都会最终影响排名和结果的发布~!到底最后怎么发布也有学问,大家好好学吧!
加法原则:取长补短,互有补充!
乘法原则:一损俱损,不可或缺!
上面的排名还没有考虑指标的标准化问题,以及如何标准化:插值法,最大值最小值法,理想点法等等!
排名是技术,发布是艺术!




 一起调研网新浪微博
一起调研网新浪微博
 一起调研网腾讯微博
一起调研网腾讯微博
